Decadimento Radioattivo nel combustibile nucleare irraggiato
di Ing. Angelo Papa, Paolo Allievi, Marco Nasta
Indice.
2 L’elemento di combustibile nucleare.
3 Il decadimento radioattivo e le reazioni nucleari indotte da neutroni.
3.2 Reazioni nucleari indotte da neutroni.
4
Creazione e decadimento di isotopi radioattivi
![]() nel combustibile (nel reattore e fuori). Modellizzazione
matematica del processo fisico.
nel combustibile (nel reattore e fuori). Modellizzazione
matematica del processo fisico.
5 Codice di calcolo utilizzato per la valutazione dell’inventario isotopico del combustibile irraggiato SOGIN.
6 Esempi di valutazione dell’inventario isotopico sul combustibile irraggiato SOGIN.
1 Introduzione.
In questa relazione viene discussa la modellizzazione matematica dei fenomeni di creazione e decadimento degli isotopi radioattivi all’interno di un elemento di combustibile nucleare irraggiato durante la sua permanenza nel reattore e nel successivo periodo di raffreddamento fuori dal nocciolo.
Viene illustrato poi come l’evoluzione temporale della concentrazione di tutti i nuclidi presenti nel combustibile nucleare (“evoluzione isotopica del combustibile”) può essere determinata risolvendo le equazioni risultanti dal modello.
In particolare è presentata una sequenza di codici di calcolo (SAS2H [2]) che implementa un algoritmo che fornisce la soluzione del problema in esame.
Vengono riportati a titolo di esempio i risultati ottenuti dall’applicazione della suddetta sequenza di codici di calcolo al combustibile irraggiato nella centrale nucleare di Caorso.
Prima di descriverne la modellizzazione matematica, viene data una breve descrizione dell’elemento di combustibile nucleare e dei fenomeni fisici che in esso avvengono durante l’irraggiamento nel reattore e nella successiva fase di raffreddamento.
2 L’elemento di combustibile nucleare.
L’elemento di combustibile rappresenta il componente fondamentale di un impianto nucleare. Esso contiene infatti il materiale fissile che da luogo alle reazioni di fissione con conseguente liberazione di energia (circa 200 MeV per evento di fissione).
Nella tipologia più affermata di impianto nucleare (reattore ad acqua leggera LWR), (impianti di Trino, Caorso, Garigliano) l’elemento di combustibile è costituito da un fascio di barrette disposte solitamente a formare un reticolo quadrato, e tenute assieme da elementi strutturali quali griglie distanziatici e piastre terminali superiore ed inferiore (Vedi figura 2.1).
All’interno di ciascuna barretta, costituita da un tubo metallico (inox, lega di zirconio, etc.) è contenuto il combustibile nucleare vero e proprio, ossia l’uranio (ed eventualmente il plutonio in caso di MOX) sotto forma di ossido (UO2, PuO2), e arricchito nel suo isotopo fissile U-235 (arricchimenti tipici dell’uranio in reattori LWR variano tra il 2% e il 5%, contro un’abbondanza di appena lo 0.7% dell’isotopo U-235 nell’uranio naturale).
Gli elementi di combustibile sono sistemati all’interno del reattore nucleare a formare il nocciolo del reattore. Nei reattori tipici reattori LWR di concezione occidentale, il reattore è costituito da un grosso cilindro in acciaio in cui sono alloggiati gli elementi di combustibile immersi in acqua. L’acqua svolge funzione sia di moderatore neutronico (reattori termici) che di fluido termovettore. L’acqua, infatti circolando all’interno del reattore, e lambendo le barrette di combustibile asporta il calore prodotto a seguito delle reazioni di fissione che avvengono nella matrice di ossido di uranio.
In condizioni di funzionamento del reattore, l’elemento di combustibile è sottoposto ad un flusso neutronico, generato proprio dai neutroni prodotti dagli eventi di fissione (in ogni evento di fissione si liberano infatti 2-3 neutroni).
Questo flusso neutronico è necessario a generare successive fissioni all’interno del combustibile nucleare. Nel caso in cui i neutroni di una generazione sono pari ai neutroni della generazione successiva, la reazione di fissione si autosostiene e il reattore si dice critico.
Oltre alle reazioni di fissione, all’interno del combustibile nucleare avvengono numerose altre trasformazioni nucleari che interessano gli atomi dei materiali presenti.
Gli isotopi creati a seguito di una fissione sono infatti altamente instabili dal punto di vista nucleare e danno pertanto origine a catene di decadimenti radioattivi. La presenza di un flusso neutronico inoltre da luogo ad interazioni (cattura neutronica, etc.) con molti degli elementi presenti con creazione di nuovi isotopi generalmente instabili che a loro volta decadono originandone altri. Si ha pertanto una evoluzione isotopica del combustibile durante il suo periodo di irraggiamento nel reattore, evoluzione che continua anche dopo lo scarico del combustibile dal reattore. Quando il combustibile non è più nel reattore, infatti, anche se non è più soggetto ad irraggiamento neutronico, continuano le reazioni di decadimento degli isotopi radioattivi creati nella precedente fase di irraggiamento. Poiché ad ogni decadimento è associata liberazione di energia, il combustibile, anche fuori dal reattore, continua ad a produrre calore, da ciò la necessità di continuare ad asportare tale calore di decadimento anche una volta che l’elemento è stato estratto dal nocciolo.
Negli elementi di combustibile è contenuta più del 99% della radioattività tipicamente presente su tutto un impianto nucleare.
Figura 2.1 – Tipico elemento di combustibile di un reattore BWR

3 Il decadimento radioattivo e le reazioni nucleari indotte da neutroni.
Prima di presentare il problema dell’evoluzione temporale della composizione radioisotopica del combustibile nucleare irraggiato, viene qui presentato un breve panorama delle reazioni che tale evoluzione determinano.
3.1 Decadimento radioattivo.
Il decadimento radioattivo è un processo che interessa il nucleo dell’atomo. Esistono vari tipi di decadimento radioattivo, tutti dovuti ad un’instabilità nucleare del nucleo che decade. La stabilità di un nucleo è data da un equilibrio tra il numero dei due tipi di nucleoni (neutroni e protoni) che lo compongono. Nuclei instabili sono quelli caratterizzati dalla presenza in eccesso di uno dei due tipi di nucleoni rispetto alla situazione di equilibrio. La carta dei nuclidi in figura 1.1 mostra i nuclidi stabili in funzione del numero dei neutroni e dei protoni nel nucleo.
Figura 3.1

I tipi più comuni di decadimento radioattivo sono:
1) Fissione spontanea (transuranici, nuclei con numero di massa elevato):
N1 (A1, Z1) → N2 (A2, Z2) + N3 (A3, Z3) + ξn
con ξ resa neutronica della fissione (2÷3).
2) Decadimento alfa: N1 (A, Z)→ N2 (A-4 , Z-2) + α
con α nucleo di 4He
3) Decadimento beta positivo: N1 (A, Z) → N2 (A, Z-1) + e+ + νe
con e+ positrone e νe neutrino elettronico
4) Cattura elettronica: N1 (A, Z) + e-→ N2 (A, Z-1) + νe
con e- elettone e νe neutrino elettronico
5) Decadimento beta negativo: N1 (A, Z)→ N2 (A, Z+1) + e- + νe*
con e- elettone e νe* antineutrino elettronico
6) Decadimento γ: N1* (A, Z) → N1 (A, Z)
Ciascun decadimento di tipo alfa, beta, cattura elettronica o fissione spontanea solitamente è accompagnato da emissione di radiazione elettromagnetica γ (decadimento γ) a seguito di riassestamento dei nucleoni nei livelli energetici nucleari del nucleo figlio e/o radiazione X (energia elettromagnetica) a seguito di riassestamento degli elettroni nei livelli energetici orbitali del nucleo figlio.
La radioattività naturale è nota fin dal 1896, quando Becquerel trovò che i composti dell’uranio emettevano radiazioni penetranti simili ai raggi X.
Se N il numero di atomi di un radioisotopo presenti al tempo t, uno studio statistico del decadimento radioattivo ha mostrato che il numero di disintegrazioni che si verificano nell’unità di tempo è proporzionale al numero totale di atomi radioattivi presenti, cioè:
![]() (3.1)
(3.1)
dove ![]() è la costante del decadimento radioattivo tipica
dell’elemento radioattivo e
è la costante del decadimento radioattivo tipica
dell’elemento radioattivo e ![]() è la sua vita media. Si definisce, inoltre, T1/2 =
tempo di dimezzamento dell’elemento, pari al tempo necessario affinché il
suo numero di atomi si dimezzi. Si ha: T1/2=ln(2)
è la sua vita media. Si definisce, inoltre, T1/2 =
tempo di dimezzamento dell’elemento, pari al tempo necessario affinché il
suo numero di atomi si dimezzi. Si ha: T1/2=ln(2) ![]()
La legge del decadimento radioattivo è dunque, integrando la (3.1) e con N0 numero iniziale di atomi del radioisotopo:
![]() (3.2)
(3.2)
Si definisce attività del radionuclide la seguente grandezza, funzione del tempo, che esprime il numero di decadimenti nell’unità di tempo:
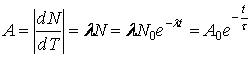 (3.3)
(3.3)
Un nucleo radioattivo può, in generale, decadere in un nucleo figlio anch’esso instabile che decade a sua volta, e così via fine a giungere ad un nucleo figlio stabile. Tale sequenza di decadimenti viene definita catena di decadimento o famiglia radioattiva.
Consideriamo la famiglia radioattiva di figura 3.2.
Figura 3.2
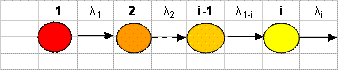
Prendiamo in considerazione l’iesimo membro, il cui numero di atomi Ni può essere calcolato per mezzo della seguente equazione differenziale:
![]() (3.4)
(3.4)
che esprime il bilancio tra i radioisotopi i prodotti nell’unità di tempo per decadimento dei radioisotopi i-1 ed i radioisotopi i persi nell’unità di tempo per decadimento verso i radioisotopi i+1.
La (3.4), scritta per tutti i radioisotopi della catena di decadimento, rappresenta un sistema di equazioni differenziali ordinario, del primo ordine, lineare, a coefficienti costanti e omogeneo, di forma particolarmente semplice (matrice di transizione del sistema bidiagonale, vedi capitolo 3 dove vengono trattati sistemi più complessi). Risolvendo tale sistema è possibile trovare il numero Ni di atomi dell’iesimo membro della famiglia in funzione del tempo.
Nel caso in cui il numero di atomi iniziale
di tutti i membri della famiglia sia uguale a zero tranne quelli del
capostipite pari a ![]() , la soluzione può essere messa nella seguente forma
(vedi: H. Bateman [1]):
, la soluzione può essere messa nella seguente forma
(vedi: H. Bateman [1]):
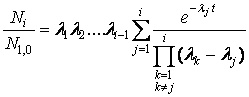 (3.5)
(3.5)
Nel caso di una famiglia radioattiva composta da soli 2 radioisotopi che decadono e un terzo finale stabile, la (3.5) conduce a:
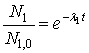 (3.6)
(3.6)
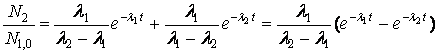 (3.7)
(3.7)
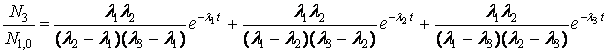 (3.8)
(3.8)
Ed essendo ![]() , si ha:
, si ha:
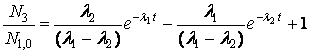 (3.8’)
(3.8’)
Ricavando dalla (3.6) e dalla (3.7) le attività dei due radionuclidi instabili della catena si ha:
![]()
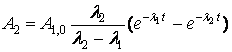 (3.9)
(3.9)
In funzione del rapporto tra le costanti di
decadimento ![]() 1 e
1 e ![]() 2 dei primi due isotopi della famiglia, possono
presentarsi tre particolari situazioni:
2 dei primi due isotopi della famiglia, possono
presentarsi tre particolari situazioni:
1) ![]() 2 >>
2 >> ![]() 1: equilibrio secolare
1: equilibrio secolare
Su tempi di osservazione brevi rispetto alla vita media del nuclide N1, l’attività del nuclide N1 può essere considerata costante, e le (3.9) possono essere approssimate dalle seguenti:
![]() = costante
= costante
![]()
Dopo pochi tempi di dimezzamento del nuclide N2, si raggiunge la situazione di equilibrio A1=A2.
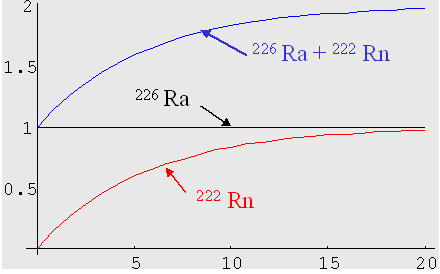
Un esempio di equilibrio secolare è
rappresentato dai due nuclidi ![]() (T1/2=1602 anni) e il suo figlio
(T1/2=1602 anni) e il suo figlio ![]() (T1/2=3.8 giorni)
(T1/2=3.8 giorni)
L’andamento con il tempo delle attività (considerando un’attività iniziale del nuclide padre uguale ad uno nell’unità di misura scelta) è riportato in figura 3.3
Figura 3.3
Attività [Bq]
Tempo [giorni]
2) ![]() 2 >
2 > ![]() 1: equilibrio transitorio:
1: equilibrio transitorio:
E’ la situazione in cui il tempo di dimezzamento del nuclide padre è dell’ordine di grandezza del tempo di osservazione mentre quello del nuclide figlio è considerevolmente più corto ma non trascurabile come nel caso precedente. Dalle (3.9) in questo caso si ha:
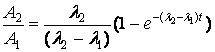
L’attività del nuclide figlio passa
attraverso un massimo, dopodichè decresce con lo stesso rateo del nuclide
padre. L’equilibrio è raggiunto per (![]() 2 -
2 -![]() 1) t >> 1, tempo dopo il quale si ha:
1) t >> 1, tempo dopo il quale si ha:
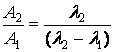
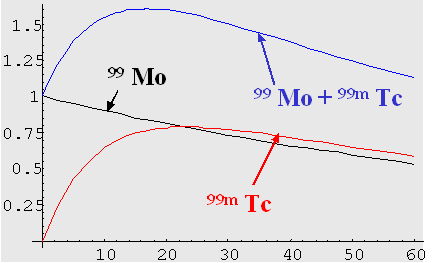
Un buon esempio di equilibrio transitorio è
fornito dal ![]() (T1/2=66.7 ore) e dal suo figlio
(T1/2=66.7 ore) e dal suo figlio ![]() (T1/2=6.02 ore).
(T1/2=6.02 ore).
L’andamento con il tempo delle attività (considerando un’attività iniziale del nuclide padre uguale ad uno nell’unità di misura scelta) è riportato in figura 3.4
Figura 3.4
Attività [Bq]
Tempo [ore]
3) ![]() 2 <
2 < ![]() 1: Non equilibrio
1: Non equilibrio
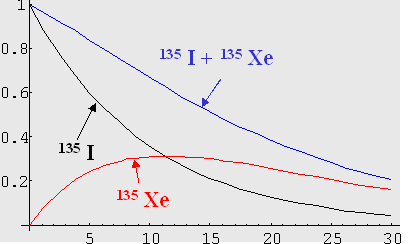
In questo caso non si stabilisce alcun equilibrio tra l’attività del nuclide padre e quella del nuclide figlio. Mentre l’attività del nuclide padre decresce, quella del nuclide figlio parte da zero, aumenta fino ad un massimo, dopodichè decresce più lentamente con il suo rateo di decadimento.
Un esempio di tale situazione è fornito
dallo ![]() (T1/2=6.7 ore) e dal suo figlio
(T1/2=6.7 ore) e dal suo figlio ![]() (T1/2=9.2 ore).
(T1/2=9.2 ore).
L’andamento con il tempo delle attività (considerando un’attività iniziale del nuclide padre uguale ad uno nell’unità di misura scelta) è riportato in figura 3.5.
Figura 3.5
Attività [Bq]
Tempo [ore]
3.2 Reazioni nucleari indotte da neutroni.
Ciascun elemento, sottoposto ad un flusso neutronico presenta una probabilità più o meno elevata (anche nulla) di interagire con un neutrone (n)
Tali interazioni, che dipendono dall’energia dei neutroni in gioco, possono essere di assorbimento, o di semplice urto (elastico o anelastico).
A seguito dell’assorbimento neutronico un nucleo può dar luogo a fissione indotta, a cattura del neutrone (con emissione di radiazione γ) o a espulsione di altri nucleoni (reazioni (n,2n) (n,3n) (n,p) etc.).
La probabilità di accadimento di un tale reazione è legata alla natura del nucleo e all’energia del neutrone e può essere determinata tramite equazioni, che data la natura microscopica del fenomeno in esame, coinvolgono l’utilizzo della meccanica quantistica. Il risultato di tali equazioni può essere sintetizzato da una grandezza chiamata sezione d’urto microscopica del nucleo per la determinata reazione neutronica. La sezione d’urto è funzione dell’energia del neutrone. Definita la sezione d’urto, che esprime, come detto, la probabilità di accadimento della reazione, il rateo di reazioni in un materiale sottoposto ad irraggiamento neutronico può essere espresso nel modo seguente:
R = σ(E) N Φ(E) = Σ(E) Φ(E)
dove:
σ(E) = sezione d’urto microscopica funzione dell’energia [cm2]
N = Densità del nuclide (nuclei per unità di volume) [atomi/cm3]
Φ(E) = flusso neutronico [n/cm2 s]
Σ(E) = sezione d’urto macroscopica funzione dell’energia [atomi/cm]
I nuclei prodotti a seguito di interazioni con neutroni sono, generalmente, instabili e soggetti ad uno dei tipi di decadimento radioattivo esposti nel paragrafo precedente.
4
Creazione e decadimento di isotopi
radioattivi  nel combustibile (nel reattore e fuori). Modellizzazione
matematica del processo fisico.
nel combustibile (nel reattore e fuori). Modellizzazione
matematica del processo fisico.
Come detto, in un elemento di combustibile nucleare all’interno del reattore, per via delle reazioni nucleari attivate dal flusso neutronico (fissione, cattura, etc.) e dei processi di decadimento radioattivo dei nuclei instabili, avviene una vera e propria evoluzione temporale dell’inventario isotopico.
La variazione della quantità di un qualunque nuclide presente in un determinato istante nel combustibile può essere ricavata da un bilancio tra il suo tasso di creazione e suo tasso di scomparsa. Si ha per il generico isotopo i:
![]()
![]()
Che può essere espresso tramite la seguente formula:
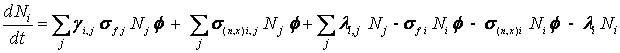 (4.1)
(4.1)
con i e j da 1 a M = numero di isotopi presenti.
I simboli introdotti hanno il seguente significato:
Ni = densità atomica del generico isotopo i
σf j = sezione d’urto di fissione dell’isotopo j
γi,j = probabilità di creazione dell’isotopo i dalla fissione dell’isotopo j
σ(n,x) i, j = sezione d’urto di reazione (n,x) (compresa cattura radiativa) sull’isotopo j che dia luogo alla creazione dell’isotopo i
λi,j = costante di decadimento dell’isotopo j nell’isotopo i
σf i = sezione d’urto di fissione dell’isotopo i
σ(n,x) i = sezione d’urto di reazione (n,x) (compresa cattura radiativa) dell’isotopo i
λi = costante di decadimento complessiva dell’isotopo i
Φ = flusso neutronico
I termini dell’equazione (4.1) hanno il seguente significato fisico:
![]() è il tasso di formazione dell’isotopo i dovuto
alla fissione di tutti gli altri isotopi che possono dar luogo a fissione
è il tasso di formazione dell’isotopo i dovuto
alla fissione di tutti gli altri isotopi che possono dar luogo a fissione
![]() è il tasso di formazione dell’isotopo i dovuto
alle reazioni neutroniche di assorbimento (esclusa la fissione) su tutti
gli alti isotopi
è il tasso di formazione dell’isotopo i dovuto
alle reazioni neutroniche di assorbimento (esclusa la fissione) su tutti
gli alti isotopi
![]() è il tasso di formazione
dell’isotopo i dovuto al decadimento radioattivo di tutti gli altri
isotopi
è il tasso di formazione
dell’isotopo i dovuto al decadimento radioattivo di tutti gli altri
isotopi
![]() è il tasso di scomparsa
dell’isotopo i dovuto a fissione dell’isotopo i (se fissionabile)
è il tasso di scomparsa
dell’isotopo i dovuto a fissione dell’isotopo i (se fissionabile)
![]() è il tasso di scomparsa dell’isotopo i
dovuto ad assorbimento neutronico sull’isotopo i
è il tasso di scomparsa dell’isotopo i
dovuto ad assorbimento neutronico sull’isotopo i
![]() è il tasso di scomparsa
dell’isotopo i dovuto a decadimento radioattivo dell’isotopo i
è il tasso di scomparsa
dell’isotopo i dovuto a decadimento radioattivo dell’isotopo i
Quando il combustibile viene estratto dal reattore, essendo nullo il flusso neutronico a cui esso è soggetto, dalla (4.1) scompaiono i termini legati alle trasformazioni indotte dalle interazioni nuetroniche e rimangono presenti solo quelle associate ai decadimenti dei nuclei instabili:
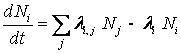 (4.2)
(4.2)
Il vettore N = (N1, N2,…..Ni,…..Nn) che rappresenta le densità atomiche degli isotopi presenti, e le cui componenti sono espresse dall’equazione (4.1), dipende, in generale, oltre che dal tempo, dalla posizione all’interno dell’elemento di combustibile: N = N(x,y,z,t)
Il flusso neutronico che compare nella equazione (4.1) è, in generale, funzione del tempo, potendo variare la potenza a cui funziona il reattore, e funzione della concentrazione di tutti gli isotopi presenti, ossia del vettore N. L’intensità del flusso, inoltre, varia in funzione dell’energia dei neutroni. Nel caso generale si ha pertanto per il flusso:
Φ = Φ[E,N(x,y,z,t),t] (4.3)
Le sezioni d’urto di fissione e di cattura neutronica, proporzionali alla probabilità che avvenga la relativa reazione, dipendono invece dall’energia del neutrone interagente:
σc = σc(E); σf = σf(E).
Considerando una determinata posizione all’interno dell’elemento di combustibile, se la (4.1) viene scritta per tutti gli isotopi presenti in tale posizione (che possono essere dell’ordine delle centinaia), si può notare che il problema dell’evoluzione temporale della concentrazione dei vari nuclidi in un punto (si assume che non vi sia migrazione di isotopi all’interno della matrice del combustibile) all’interno del combustibile nucleare è definito da un sistema di equazioni differenziali del primo ordine omogeneo.
Al fine di evitare un calcolo punto per punto dell’evoluzione isotopica nel combustibile, in realtà conviene suddividere l’elemento in zone in cui si può supporre una variazione spaziale del vettore N limitata, e affrontare il problema dell’evoluzione temporale della densità dei vari radionuclidi mediata in ciascuna delle zone di suddivisione. In tal modo può essere eliminata la dipendenza spaziale del vettore N. L’ampiezza delle zone di suddivisione dipende dalla particolare applicazione per cui si richiede il calcolo di N. Per molte applicazioni è sufficiente studiare l’andamento temporale della concentrazione dei vari nuclidi mediata su tutto l’elemento di combustibile.
In seguito per N si intenderà il vettore delle concentrazioni degli isotopi mediate sull’intero elemento di combustibile e non si considererà più la dipendenza spaziale di N. Di conseguenza anche il flusso neutronico sarà quello medio all’interno dell’elemento.
Data la dipendenza funzionale del flusso dal vettore delle concentrazioni isotopiche, e dal tempo, il sistema definito dalle equazioni (4.1), è un sistema di equazioni differenziali del primo ordine omogeneo, non lineare e non è risolvibile in forma esplicita.
Al fine di cercare soluzioni esplicite al problema è necessario eliminare la dipendenza del flusso da N, che corrisponde a linearizzare il sistema di equazioni differenziali.
Ciò può essere fatto assumendo che tale dipendenza del flusso da N sia trascurabile in un intervallo di tempo Δt sufficientemente piccolo intorno al tempo t0. In tale intervallo il flusso neutronico può essere approssimato con il flusso calcolato a partire dal vettore N(t0).
Mediando poi il flusso così calcolato sull’energia:
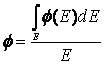 (4.3’)
(4.3’)
e definendo come sezione d’urto mediata sul flusso la seguente grandezza:
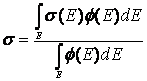 (4.3’’)
(4.3’’)
per l’intervallo temporale Δt, la (4.1) assume la forma di un sistema di equazioni differenziali ordinario del primo ordine lineare. Se si assume inoltre che per il flusso nell’intervallo Δt possa essere trascurata anche la dipendenza esplicita dal tempo che figura nella (4.3) (flusso costante nell’intervallo Δt), il sistema (4.1) diviene un sistema di equazioni differenziali ordinario del primo ordine omogeneo lineare e a coefficienti costanti.
La soluzione di tale sistema semplificato, fornisce il vettore N all’istante t1=t0+Δt, a partire dalle concentrazioni isotopiche all’istante t0: N(t0)
Dal vettore N(t1) si può poi calcolare il flusso all’istante t1, e da questo ripetere il processo per calcolare il vettore N all’istante t2=t1+Δt. Iterando tale processo è dunque possibile calcolare il vettore N ad ogni istante temporale.
Il problema del calcolo dell’evoluzione temporale delle concentrazioni isotopiche è stato dunque ridotto alla risoluzione di un sistema di equazioni differenziali del primo ordine, omogeneo, lineare a coefficienti costanti.
Tale sistema può essere espresso nella seguente forma:
![]()
![]() (4.4)
(4.4)
Dove ![]() è la derivata rispetto al tempo del vettore delle
concentrazioni isotopiche e A è la matrice di transizione del
sistema.
è la derivata rispetto al tempo del vettore delle
concentrazioni isotopiche e A è la matrice di transizione del
sistema.
Come si può notare analizzando l’equazione (4.1), la matrice A è una matrice quadrata di dimensioni M x M (con M numero di nuclidi presenti) e contiene le costanti di decadimento e i coefficienti di reazione neutronica:
ai,j = γi,j σf j Φ + σ(n,x)i, j Φ + λi,j
ai,i = - σf i Φ – σ(n,x) i Φ – λi
Nell’intervallo Δt, tutti gli elementi di A sono costanti, in quanto determinati per un flusso supposto costante durante tale intervallo e pari a Φ(t=0).
Il sistema (4.4), con A matrice ad elementi costanti, ha la nota soluzione:
![]() (4.5)
(4.5)
Dunque, il problema ai valori iniziali (problema di Cauchy) definito dal sistema di equazioni differenziali (4.4) e da N(0) vettore delle concentrazioni isotopiche iniziali all’istante t=t0, ha come soluzione (unica):
![]() (4.6)
(4.6)
dove, in analogia alla definizione di funzione esponenziale nel caso di variabile singola, la funzione esponenziale di matrice può essere definita tramite la seguente serie di funzioni (uniformemente convergente):
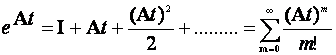 (4.7)
(4.7)
Con I matrice unitaria.
Per tale esponenziale di matrice, si può dimostrare che valgono molte delle proprietà tipiche dell’esponenziale di una grandezza scalare.
La soluzione (4.6) può essere espressa sottoforma di sommatoria di un numero finito di termini solo se si conoscono tutti gli autovalori della matrice A.
Nel caso di autovalori reali e distinti, ad esempio, la matrice A può essere espressa nella seguente forma:
A = B D B-1 (4.8)
Con D matrice diagonale M x M con gli elementi sulla diagonale principale uguali agli autovalori di A, e B matrice M x M le cui colonne sono gli autovettori corrispondenti agli autovalori di A.
Con A data dalla (4.8), si può dimostrare che:
![]() (4.9)
(4.9)
Essendo poi l’esponenziale di una matrice diagonale uguale ad una matrice diagonale con elementi sulla diagonale rispettivamente uguali all’esponenziale degli elementi diagonali della matrice iniziale, ossia:
 (4.10)
(4.10)
con μ1…. μM = autovalori reali e distinti di A,
si ha che la soluzione del sistema (4.4) in questo caso è data dal seguente prodotto tra matrici:
N = B F B-1 N(0). (4.11)
Nel caso di elemento di combustibile fuori dal reattore, come già detto, le equazioni alla base dell’evoluzione temporale del vettore delle concentrazioni isotopiche sono quelle descritte dalla (4.2), che rappresentano una semplificazione della (4.1) dovuta alla assenza di reazioni neutroniche e alla presenza di solo decadimento. In assenza di reazioni neutroniche, ciascun nuclide non può in nessun modo essere generato da un nuclide prodotto dal suo precedente decadimento. Ciò equivale a dire che le catene di decadimento non presentano in tale caso fenomeni di loop.
Dal punto di vista della modellizzazione matematica, ciò equivale a dire che la matrice di transizione del sistema in questo caso è una matrice triangolare.
Gli elementi sulla diagonale principale sono pertanto gli autovalori della matrice. In questo caso l’autovalore μi è uguale alla costante di decadimento dell’iesimo nuclide cambiata di segno –λi. Nel caso di costanti di decadimento tutte diverse tra loro (autovalori distinti), la matrice A può essere diagonalizzata usando la matrice B degli autovettori associati.
Nel caso ancor più semplice di assenza di reazioni neutroniche e di catene di decadimento lineari e indipendenti, ossia definite dalla condizione che ogni isotopo può decadere in un solo nuclide figlio, e che non vi sono legami tra tali catene di decadimento, la matrice A, diviene una matrice bidiagonale.
In questo caso ricade anche il caso di singola catena di decadimento lineare (equazione di Bateman) visto nel capitolo 3. Se le costanti di decadimento di tutti gli isotopi della catena sono differenti tra loro (autovalori di A distinti) si può dimostrare che la componente iesima del vettore N assume la forma:
![]()
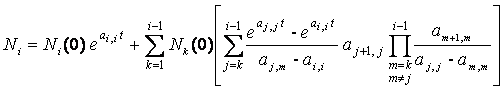 (4.12)
(4.12)
con i da 1 a M, numero degli elementi della catena di decadimento.
In questo caso l’elemento iesimo della diagonale principale della matrice A, ossia ai,i è uguale a -λi, costante di decadimento dell’elemento iesimo cambiata di segno, e l’elemento aj+1,j della diagonale secondaria è pari a λj, costante di decadimento dell’elemento jesimo. Pertanto la (4.12) può essere scritta come:
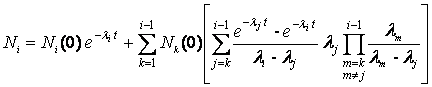
Nel caso in cui la concentrazione iniziale i tutti i nuclidi della catena, tranne quella del nuclide capostipite, sia uguale a zero, si ha la soluzione di Bateman riportata nel paragrafo 3.2.
Ritornando al caso di combustibile nel reattore, in generale la matrice di transizione A può avere autovalori non tutti reali e/o con molteplicità maggiore di uno, si può comunque dimostrare che, conoscendo tali autovalori, l’esponenziale della matrice A può essere sempre ridotta ad una somma con numero finito di prodotti di matrici (La matrice A può essere infatti sempre scomposta in una matrice semisemplice, diagonalizzabile cioè in senso complesso, e in una nilpotente, il cui esponenziale da un certo esponente in poi è pari a zero. L’esponenziale di entrambe queste matrici è esprimibile in sottoforma di sommatoria di un numero finito di termini).
L’espressione sottoforma di sommatoria con numero finito di termini della soluzione analitica per il vettore delle concentrazioni isotopiche all’istante t1=t0+Δt, comporta pertanto il calcolo degli autovalori della matrice A.
Data la notevole dimensione della matrice A (il numero degli isotopi in considerazione è di diverse centinaia), tale calcolo non è per niente agevole.
Nella pratica per il calcolo del vettore N si adottano algoritmi di calcolo numerico che forniscono una soluzione sufficientemente approssimata del problema ma che sono più efficienti dal punto di vista computazionale.
Nel capitolo successivo verrà presentato l’approccio numerico per il calcolo di N utilizzato dal codice di calcolo ORIGEN-S [4], codice ampiamente utilizzato per le valutazioni dell’inventario isotopico del combustibile irraggiato negli impianti della SOGIN.
5 Codice di calcolo utilizzato per la valutazione dell’inventario isotopico del combustibile irraggiato SOGIN.
Sono stati sviluppati svariati codici di calcolo che, in base alla modellizzazione matematica esposta nel paragrafo precedente, permettono di calcolare la variazione temporale delle concentrazioni di tutti i nuclidi che si creano all’interno di un elemento di combustibile nucleare irraggiato. Tutti procedono ad una linearizzazione del sistema di equazioni differenziali (4.1) in un intervallo temporale sufficientemente piccolo intorno all’istante iniziale, intervallo in cui il flusso neutronico può assumersi costante, e iterando il procedimento per intervalli temporali successivi.
Tali codici possono differenziarsi nell’approccio alla soluzione del sistema lineare a coefficienti costanti (4.4), implementando algoritmi di calcolo numerico differenti.
Per la valutazione dell’inventario isotopico del combustibile irraggiato della SOGIN è stata utilizzata la sequenza di calcolo SAS2H [2].
Si tratta di un insieme di codici di calcolo sviluppati e costantemente mantenuti dal laboratorio statunitense di Oak Ridge, e che vanta un ampio utilizzo a livello mondiale e un esteso programma di validazione tramite benchmarks sperimentali.
Vediamo ora l’approccio utilizzato dal software in esame per la soluzione del problema dell’evoluzione temporale delle concentrazioni isotopiche nel combustibile nucleare irraggiato.
Come prima semplificazione viene eliminata la dipendenza delle concentrazioni isotopiche dalle coordinate spaziali, suddividendo l’analisi per zone sufficientemente omogenee.
Si valuta pertanto l’evoluzione temporale della concentrazione media dei nuclidi all’interno di ciascuna di tali zone. Per le applicazioni più comuni, come già detto, una zona può coincidere con l’intero elemento di combustibile.
Viene poi effettuata una discetizzazione in intervalli temporali di lunghezza opportuna della storia di irraggiamento dell’elemento di combustibile in esame. Sia i cicli di irraggiamento nel reattore, sia i successivi periodi con reattore spento tra un ciclo e l’alto e sia il tempo di raffreddamento finale dallo scarico finale dell’elemento dal nocciolo vengono suddivisi in un numero adeguato di step temporali.
La sequenza SAS2H, si compone di svariati codici di calcolo e utilities per i trasferimento automatico di dati da un codice all’altro.
I codici fondamentali della sequenza sono quello che effettua il calcolo del flusso per ciascun intervallo temporale (XRDRNPM [3]) e quello che calcola il vettore delle concentrazioni isotopiche alla fine di ciascun intervallo temporale risolvendo il sistema differenziale linearizzato (4.4) (ORIGEN-S [4]).
La sequenza di calcolo è percorsa in modo iterativo. A partire dalla concentrazione isotopica iniziale e dalla potenza termica dell’elemento di combustibile nel primo intervallo temporale (supposta costante in ciascun intervallo temporale), XRDRNPM determina lo spettro energetico del flusso neutronico applicabile al primo intervallo temporale. Tale spettro energetico del flusso viene utilizzato, assieme a dati sulle sezioni d’urto microscopiche (contenute in files di librerie di dati nucleari distribuite con il codice), per determinare il flusso medio sull’energia e le sezioni d’urto medie pesate sul flusso (vedi (4.3’) e (4.3’’)) per ciascun tipo di reazione e per ciascun nuclide presente. Da questi dati è possibile costruire la matrice di transizione a coefficienti costanti A per il sistema linearizzato nel primo intervallo temporale. Dalla matrice A e dal vettore delle concentrazioni iniziali N(t0)=N0, il codice ORIGEN-S, tramite l’algoritmo numerico illustrato in seguito, determina il vettore delle concentrazioni isotopiche N(t1) all’istante finale dell’intervallo temporale. Tale valore del vettore N(t1), assieme alla potenza termica dell’elemento di combustibile nel secondo intervallo temporale, viene processato nuovamente dal codice XRDRNPM per determinare lo spettro del flusso per il secondo intervallo. Da questo si ricava la matrice di transizione per il secondo intervallo e una seconda applicazione di ORIGEN-S fornisce il vettore N(t2) alla fine del secondo intervallo. Il processo viene ripetuto per tutti gli intervalli in cui si è discretizzata l’evoluzione temporale. Durante gli intervalli fuori dal reattore, nella matrice A non compaiono ovviamente i termini dovuti all’irraggiamento neutronico. La sequenza è rappresentata tramite schema a blocchi a scopo esplicativo nella figura 5.1[1]
![]()
|
|
Figura 5.1
![]()
|
|


N0 = vettore concentrazioni isotopiche iniziali (input)
Pi = Potenza dell’elemento in Δti+1 (input)
Ni = vettore concentrazioni isotopiche all’istante i
Фi(E) = spettro energetico flusso neutronico all’istante i
σ(E) = sezioni d’urto funzione di E neutroni (da librerie dati nucleari)
Фi = flusso neutronico mediato su E all’istante i
σi = sezioni d’urto pesate sul flusso all’istante i
Ai = matrice di transizione per l’intervallo Δti
Il codice ORIGEN-S può essere utilizzato anche da solo, ossia all’esterno della sequenza SAS2H. Il tal caso non viene calcolato lo spettro energetico del flusso derivante dalla specifica composizione isotopica del combustibile. Come input viene fornita la potenza dell’elemento di combustibile (legata all’intensità di flusso dei neutroni termici) nei vari intervalli temporali in cui si suddivide l’evoluzione temporale.
Quando l’ORIGEN è utilizzato da solo, l’input (potenza dell’elemento o direttamente flusso neutronico) fornisce l’intensità del flusso dei neutroni termici (energia compresa tra 0 e 0.625 eV). Come spettro energetico di base per il flusso neutronico, viene utilizzato quello che mediamente si ha nei reattori nucleari termici.
Le sezioni d’urto pesate sul flusso sono calcolate a partire dalle sezioni d’urto microscopiche di ciascun elemento e utilizzando lo spettro tipico dei reattori termici. Utilizzando altri due parametri di input può essere modificato il peso relativo nello spettro energetico del flusso, della regione energetica delle risonanze (energia tra 0.625 eV e 1 MeV) e della regione dei neutroni cosiddetti veloci (energia > 1 MeV).
Come visto nel paragrafo precedente, per esprimere la soluzione del sistema linearizzato (4.4) come somma finita di termini, occorre determinare tutti gli autovalori della matrice di transizione A. Le dimensioni della matrice, pari al numero dei nuclidi presenti nel combustibile, rende tale calcolo proibitivo e oltretutto poco efficiente dal punto di vista computazionale.
Il problema della soluzione del sistema di equazioni differenziali del primo ordine lineari e a coefficienti costanti (4.4) è affrontato perciò dal codice ORIGEN-S tramite un approccio differente basato su un algoritmo che permette di trovare una soluzione sufficientemente approssimata, considerando solo i primi n termini della serie definita dall’esponenziale della matrice di transizione A. Il numero di termini utilizzati è tale da far si che la soluzione trovata sia una buona approssimazione della soluzione esatta.
Dalle (4.6) e (4.7) si ha:
![]() (5.1)
(5.1)
ossia:
![]() (5.2)
(5.2)
Ogni termine della sommatoria si ottiene, cioè, dalla postmoltiplicazione della matrice A per il termine che lo precede.
Per la generica componente i del vettore N si ha:
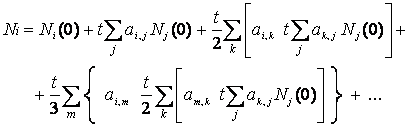 (5.3)
(5.3)
dove gli indici j,k ed m vanno da 1 a M per una matrice A di dimensioni M X M
Definendo il termine ![]() come:
come:
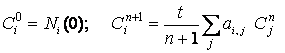 (5.4)
(5.4)
si ha che la soluzione Ni può essere espressa nel modo seguente:
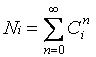 (5.5)
(5.5)
L’uso della relazione (5.5) per ottenere la
soluzione N, richiede la memorizzazione solo dei vettori ![]() e
e ![]() oltre al valore del vettore N al passo
precedente, evitando così di dover memorizzare l’intera matrice A,
che come già detto ha dimensioni notevoli.
oltre al valore del vettore N al passo
precedente, evitando così di dover memorizzare l’intera matrice A,
che come già detto ha dimensioni notevoli.
Per evitare che la grandezza relativa dei vari elementi della matrice A o che piccole differenze tra elementi positivi e negativi di A determinino una perdita inaccettabile di precisione della soluzione, nuclidi con costanti di decadimento molto grandi vengono rimossi dal sistema (e di conseguenza i corrispondenti ratei di transizione vengono rimossi dalla matrice di transizione A) e trattati separatamente.
Ad esempio, se nella catena di decadimento X → Y → Z, la costante di decadimento di B è molto grande, un nuovo rateo di transizione è inserito nella matrice per la transizione X → Z, e le transizioni X → Y e Y → Z, eliminate dal sistema vengono trattate separatamente come verrà illustrato in seguito.
La determinazioni di quali transizioni debbano essere escluse dal sistema, coinvolge il calcolo della norma della matrice di transizione A
Scelta, tra le possibili definizioni di norma la seguente (Lapidus and Luus):
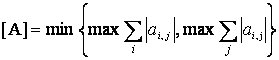 (5.6)
(5.6)
ossia il valore minimo tra la massima somma sulle righe e sulle colonne, ORIGEN fissa la seguente limitazione per la norma della matrice A:
[A] t ≤ -2 ln(0.001) =13.8155 (5.7)
Tale limitazione dipende dunque anche dall’ampiezza del passo temporale scelto.
Poiché si può dimostrare (Lapidus and Luus) che il termine massimo che figura nella sommatoria espansione della funzione esponenziale di [A] t non può superare ([A] t)n/n! dove n è l’intero più grande non maggiore di [A] t, la limitazione introdotta fa si che il massimo termine coinvolto nella sommatoria che definisce l’esponenziale della matrice A t sia dell’ordine di grandezza di 105.
Gli attuali computer essendo basati solitamente su sistemi a 32-bit (dimensione della parola) sono in grado di mantenere 16 cifre significative operando con variabili di tipo a doppia-precisione. Avendo a disposizione 16 cifre significative, e limitando il massimo termine coinvolto nella somma a valori dell’ordine di 105, il calcolo svolto mantiene cinque cifre significative fino a valori dell’ordine di 10-6. Ciò consente una adeguata precisione della soluzione ottenuta.
Il termine ai,i sulla diagonale principale della matrice A rappresenta il rateo di scomparsa complessivo (decadimento più reazioni neutroniche) dell’isotopo i. Posto ai,i = -d, la somma dei valori assoluti dei termini nella esima colonna che contiene d non può superare 2d, essendo uguale a 2d quando tutti i suoi nuclidi figli sono contenuti nel sistema (il contributo dell’isotopo iesimo alla creazione degli isotopi da lui prodotti è uguale al rateo di scomparsa dell’isotopo in questione). Da ciò e dalla (5.7) segue che:
[A] t ≤ 2d t ≤ -2 ln(0.001) (5.8)
Da quest’ultima relazione si può notare che la limitazione sulla norma della matrice A è mantenuta se si ha:
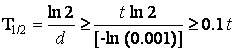 (5.9)
(5.9)
Rimuovendo cioè dal sistema i nuclidi per i quali si ha:
![]() (5.10)
(5.10)
Ossia i nuclidi per i quali il tempo di dimezzamento effettivo T1/2 è minore del 10% dell’intervallo temporale[2].
Perciò il criterio per cui un nuclide viene escluso dal sistema risolto tramite l’algoritmo descritto e trattato separatamente, dipende anche dall’intervallo temporale scelto. Diminuendo tale intervallo possono essere inclusi isotopi con tempo di dimezzamento più piccolo senza compromettere la precisione dei risultati ottenuti.
La norma della matrice A viene utilizzata anche per decidere a quale termine troncare la sommatoria (5.1) per il calcolo della soluzione.
Il numero di termini della sommatoria espansione dell’esponenziale di matrice utilizzati per il calcolo della soluzione è scelto dal ORIGEN nel modo seguente.
Il numero di termini utilizzati è pari al massimo tra: l’intero più vicino a (7/2 [A] t+6) e 21.
Tale metodo assicura un numero di termini sufficienti a limitare l’errore di troncamento a meno dello 0.1%.
Come detto, i nuclidi con tempo di dimezzamento troppo breve (in relazione al passo temporale scelto) vengono eliminati dal sistema e trattati separatamente.
Per ciascuno di tali isotopi viene infatti creata una catena di decadimento che viene studiata separatamente. Tale catena ha come capostipite il primo isotopo a lungo tempo di dimezzamento (in relazione al passo temporale scelto) che precede l’isotopo in questione, e come ultimo figlio l’isotopo a lungo tempo di dimezzamento che lo segue. Ciascuna di queste catene, che può comprendere anche più di un isotopo a breve tempo di dimezzamento eliminato dal sistema, viene supposta essere una catena lineare e ha come soluzione per la concentrazione degli isotopi che la compongono la (4.12) illustrata nel paragrafo precedente.
La matrice di transizione del sistema deve essere “aggiustata” per tener conto delle transizioni eliminate. Se ad esempio il sistema originario completo prevede le transizioni tra i nuclidi W→X→Y→Z, ed i nuclidi X e Y vengono eliminati dal sistema poiché a breve tempo di dimezzamento, nella matrice che rappresenta il sistema ridotto, comparirà un elemento che rappresenta la transizione fittizia W→Z.
Il valore di tale elemento è determinato uguagliando il valore della concentrazione dell’isotopo Z che si ottiene risolvendo l’intera catena di decadimento W→X→Y→Z tramite la (4.12) e quella che si ottiene utilizzando la sola transizione fittizia W→Z.
Tale calcolo dell’elemento da inserire nella matrice A di transizione del sistema ridotto, viene fatto prima di risolvere il sistema ridotto tramite il metodo illustrato dell’esponenziale di matrice, utilizzando come concentrazioni iniziali dei nuclidi della catena di decadimento quelle calcolate al passo precedente e supponendo nulla all’istante iniziale la concentrazione dei predecessori dell’isotopo a lungo tempo di dimezzamento W. Il valore calcolato per l’elemento della matrice approssima asintoticamente il valore corretto al crescere del numero degli intervalli temporali.
Il sistema ridotto rappresentato dalla nuova matrice A viene poi risolto con il metodo dell’esponenziale di matrice e vengono così calcolate le concentrazioni degli isotopi a lungo tempo di dimezzamento. Utilizzando poi la (4.12) si risolvono le singole catene di decadimento che comprendono gli isotopi esclusi dal sistema, determinando le loro concentrazioni al termine dell’intervallo temporale.
6 Esempi di valutazione dell’inventario isotopico sul combustibile irraggiato SOGIN.
La sequenza SAS2H è stata ampiamente utilizzata per il calcolo dell’inventario isotopico del combustibile irraggiato della SOGIN a varie date di raffreddamento.
A partire dall’inventario isotopico del combustibile ad una certa data, è infatti possibile ottenere, oltre all’attività totale nel combustibile, la potenza residua di decadimento (calore ancora prodotto dal combustibile nucleare irraggiato a seguito dei processi di decadimento dei nuclidi radioattivi in esso contenuti), nonché l’intensità della sorgente sia neutronica che fotonica (radiazione γ e X) associata all’elemento di combustibile stesso. A tal fine il codice si serve di librerie di dati nucleari in cui a ciascun nuclide è associata la propria intensità di emissione neutronica e fotonica.
Tali dati sull’intensità di emissione e sulla potenza di decadimento del combustibile sono indispensabili al fine di progettare adeguatamente i sistemi di smaltimento del calore residuo di decadimento, e degli schermi necessari ad attenuare a valori accettabili i livelli di radiazione emessi dal combustibile irraggiato.
Nelle figure seguenti vengono presentati i risultati ottenuti per l’elemento di combustibile con burnup (energia termica prodotta a fine irraggiamento per unità di peso del combustibile) maggiore (28338 MWd/tHM) (1 MWd/t = 24 kWh/kg) tra tutti i 1032 elementi irraggiati durante l’esercizio del reattore della centrale nucleare di Caorso.
Le tabella 6-1 e 6-2 riassumono le caratteristiche iniziali dell’elemento di combustibile e la sua storia di irraggiamento.
Le figure da 6-1 a 6-5 mostrano la variazione della massa di alcuni nuclidi (transuranici e prodotti di fissione) in funzione dell’irraggiamento nel reattore e del successivo periodo di decadimento.
Le figure da 6-6 a 6-9 mostrano l’andamento, in funzione del tempo di raffreddamento dallo scarico finale dell’elemento dal reattore, rispettivamente, della sorgente neutronica totale, di quella fotonica totale, della potenza residua di decadimento e dell’attività complessiva presente nell’elemento di combustibile
Tabella 6‑1 - Massa iniziale e burnup totale del combustibile dell’elemento ENA176 della centrale di Caorso
|
Massa totale elemento di combustibile [kg] |
314.9 |
|
Massa iniziale U-tot [kg] |
175.135 |
|
Massa iniziale U-235 [kg] |
4.934 |
|
Arricchimento iniziale [%] (U-235/U-tot) |
2.817 |
|
Burnup totale elemento [MWd/tHM] |
28338 |
Tabella 6‑2 - Storia di irraggiamento dell’elemento ENA176 della centrale di Caorso
|
|
Ciclo 2 |
Intervallo tra ciclo 2 e 3 |
Ciclo 3 |
Intervallo tra ciclo 3 e 4 |
Ciclo 4 |
Raffreddamento finale (al 31/12/2004) |
|
Durata [giorni] |
347 |
107 |
412 |
94 |
319 |
5564 |
|
Burnup [MWd/tHM] |
9552 |
-- |
10475 |
-- |
8311 |
-- |
|
Potenza termica [MW/elemento] |
4.821 |
-- |
4.453 |
-- |
4.563 |
-- |
Figura 6‑1

Figura 6‑2

Figura 6‑3

Figura 6‑4

Figura 6‑5

Figura 6‑6

Figura 6‑7

Figura 6‑8

Figura 6‑9

7 Riferimenti
[1] Proc. Cambridge Phil. Soc., 15, 423 (1910)
[2] ORNL/TM-2005/39 Version 5 Vol. I, Book 3, Sect. S2
[3] ORNL/TM-2005/39 Version 5 Vol. II, Book 1, Sect. F3
[4] ORNL/TM-2005/39 Version 5 Vol. II, Book 1, Sect. F7
[1] Nel testo e nel relativo diagramma di figura 5.1 viene descritto in modo semplificato il calcolo effettuato dalla sequenza SAS2H per non appesantire troppo la trattazione. In realtà intervallo temporale complessivo su cui si sta calcolando l’evoluzione della concentrazione isotopica viene percorso due volte. La prima volta, utilizzando il procedimento iterativo esposto, viene calcolato il vettore delle concentrazioni isotopiche, e quindi il flusso neutronico e le sezioni d’urto pesate sul flusso, nei punti medi di ciascun intervallo temporale in cui si è suddiviso l’intervallo complessivo. La seconda volta, per ciascun intervallo i, viene utilizzata la matrice A costruita con il flusso e le sezioni d’urto pesate sul flusso calcolate nel punto medio dell’intervallo temporale i e il vettore Ni-1 per calcolare il vettore Ni. Ciò consente di ottenere risultati più accurati, essendo il flusso e le sezioni d'urto pesate sul flusso, calcolate durante la prima passata, nel punto medio dell’intervallo più rappresentativi dei rispettivi valori medi nell’intervallo, rispetto a quelli calcolati all’inizio dell’intervallo stesso.
[2] Nel caso di discretizzazione, la variabile temporale t che figura nella (5.10) e precedenti corrisponde all’ampiezza dell’intervallo temporale Δt