L'INGANNO DEI SENSI

di Gabriele Rago - Campobasso

La fisica contemporanea, benché molti fisici anche noti ed affermati sembrino essere di parere contrario, non è affatto galileiana. Ciò, tuttavia, non vuol dire che il metodo portato alla luce da Galileo e nella sua sostanza ribattezzato modernamente "problem solving" abbia cessato di caratterizzare la Scienza e di essere pienamente valido e produttivo, ma si riferisce al fatto che la visione che oggi abbiamo del significato e delle finalità dell'attività scientifica è profondamente diversa da quella del grande pisano.

Per Galileo e per quanti ne hanno condiviso e sviluppato il pensiero esiste indiscussamente una realtà esterna allo studioso della natura, la quale è articolata secondo sue precise leggi espresse in caratteri matematici (realismo ingenuo). L'osservatore è solo un notaio della situazione il quale, se ipotizza qualcosa di suo non riferibile a questa realtà assoluta, commette un errore, che destituisce di senso e di valore il suo costrutto mentale.

Però la speculazione filosofica, che si è subito interessata criticamente del Metodo oltre che contribuire al suo affermarsi, ha messo in evidenza che al momento dell'ipotesi il soggetto costruisce di fatto una sua propria realtà, che poi prova a mettere in corrispondenza con quella esterna (dualismo cartesiano),  senza di che la conoscenza si ridurrebbe a pura e semplice abitudine mentale (scetticismo).

Senza arrivare agli estremi opposti dell'idealismo, che nega addirittura l'esistenza di una realtà esterna alla dinamica del soggetto, è già decisamente chiara e risolutiva la posizione di Emanuele Kant, il quale, pur riconoscendo a tale realtà o "cosa in sé" la funzione di stimolo alla conoscenza, in effetti poi la dichiara pensabile ma non conoscibile (noumeno) e risolve tutta l'attività conoscitiva nelle strutture che il soggetto realizza, imponendo all'esperienza le sue categorie.

D'altra parte, il sempre più frequente rivelarsi inadeguate di teorie per un certo tempo ritenute ben collaudate ed i progressi della psicologia sperimentale hanno indotto la stessa scienza galileianamente costruita a ricredersi sull'effettiva possibilità di capire un eventuale mondo esterno e di carpirne le leggi, ove mai esistessero. Si è chiaramente visto che anche il più elementare atto conoscitivo, quale è la percezione, risulta fortemente intriso di teoria, nel senso che percepiamo non ciò che è   ma ciò che vogliamo che sia,  a seconda della nostra natura, della nostra convenienza e della nostra esperienza pregressa. Una teoria rimane sempre una proposta del ricercatore che, malgrado le più o meno numerose verifiche, non potrà mai trovare una conferma definitiva (crisi dell'induttivismo ingenuo) e, con buona pace di Popper, nemmeno una falsificazione definitiva. Quelle che chiamiamo leggi dell'Universo sono in realtà strutture che noi diamo alle esperienze effettuate ed effettuabili, per  inquadrarle tutte  in uno schema coerente, anche al fine di una attendibile ma non assolutamente certa previsione (crisi del determinismo).

La Scienza, quindi, non si pone più il problema dell'esistenza e della conoscenza di una realtà assoluta, ma solo quello di costruire strutture coerenti e funzionali (realismo funzionale),  con che si colloca all'opposto dell'ormai tramontato realismo ingenuo di Galileo.

Si potrebbe obiettare che queste considerazioni sono più opportune in ambito di filosofia della Scienza ed hanno, invece, scarsa rilevanza in quella che è l'effettiva costruzione scientifica. Però a queste obiezioni si può e si deve opporre che le più caratterizzanti conquiste della fisica contemporanea quali la relatività, la quantistica ed anche le relative significative ricadute tecnologiche (si pensi all'energia nucleare) sono state rese possibili solamente perché menti arditamente creative hanno saputo concepire mondi profondamente diversi da quelli che sembravano essere suggeriti dalla comune ed ormai troppo contraddittoria evidenza sperimentale.

Se ciò è vero, è vero anche che educare i giovani alla Scienza non consiste tanto nell'imbottirli di definizioni e di leggi, quanto nel promuovere in loro adeguati atteggiamenti ed opportune consapevolezze, che li portino a vivere l'attività ed i risultati scientifici per quello che veramente sono e stanno a significare.

A dire il vero, il problema didattico è troppo ampio e complesso perché lo si possa condensare nei confini di un articolo, ma, al solo fine di chiarire il nesso tra le considerazioni fatte ed il concreto svolgersi dell'azione educativa, sarà opportuno riportare qualche esempio.

Ai problemi della percezione alcuni testi, per lo più diretti alla secondaria di primo grado, dedicano una qualche attenzione, riportando alcune situazioni già evidenziate dai gestaltisti a sostegno delle loro tesi. Fra questi il disegno mostrato in fig.1, nel quale i segmenti  AB  e  CD,  pur essendo congruenti, vengono percepiti come uno più lungo dell'altro a causa della diversa alettatura.

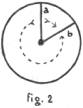
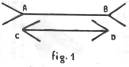
Purtroppo, però, questa situazione viene etichettata come un "inganno dei sensi", con evidente riferimento ad una realtà assoluta e incontrovertibile, che costituirebbe la verità di riferimento. Vale e dire che si omette di evidenziare come, invece, l'esigenza di una maggiore funzionalità, probabilmente suggerita dall'istinto di sopravvivenza, ci induca a valutare più l'ingombro complessivo della struttura che non la congruenza delle sue parti, cui l'ingombro stesso psicologicamente si sostituisce. Si tratta quindi di una scelta di interpretazione e di valutazione ma non di un inganno. Il preteso ricorso alla misurazione non contraddice di fatto la percezione, ma introduce nuovi diversi criteri di valutazione con diverso valore di funzionalità, che non sono, peraltro. più veri, visto che riposano sull'ammesso e mai provato postulato del trasporto rigido. Per fare ancora un altro esempio, consideriamo quel fenomeno per il quale, osservando a cinema o in televisione una carrozza che corre in avanti, si percepisce nettamente che le sue ruote stranamente girano lentamente all'indietro. Anche in questo caso gli sprovveduti potrebbero parlare di inganno, sebbene, invece, si tratti ancora una volta di una scelta di interpretazione. Infatti è noto che il moto si ricostruisce proiettando vari fotogrammi in successione. Se, quindi, (fig.2) sono a e b le posizioni di un raggio della ruota registrate in due fotogrammi successivi, queste potrebbero riferirsi tanto ad un moto progressivo che porta a in b, quanto ad un moto retrogrado più lento che fa la stessa cosa, senza che l'una situazione sia di per sé più accoglibile dell'altra. Pertanto, il soggetto che osserva sceglie istintivamente la seconda per semplici motivi di economicità. Ed infine parliamo di televisione. Certamente ognuno sarebbe disposto a giurare che le immagini più o meno colorate, di cui siamo spettatori, si formano sul piccolo schermo là dove sicuramente ci pare di vederle. Però ogni buon videotecnico sa che, di fatto, lo schermo è sempre e soltanto totalmente nero ad ogni istante, salvo un puntino, più o meno luminoso e volta per volta diversamente colorato, che lo percorre velocemente per righe da sopra a sotto, senza lasciare traccia di sé. Una macchina fotografica, che consente esposizioni inferiori al centesimo di secondo, può evidenziare questo dato di fatto. Si deve, quindi, ringraziare la persistenza delle immagini sulla retina, se sulla retina stessa può essere conservata per brevissimo tempo la storia del puntino e può perciò essere ricostruita l'immagine che poi viene riferita all'esterno. Si tratta allora di un inganno dei sensi? Certamente no!, trattandosi solo di una interpretazione inconsciamente ritenuta opportuna, anche ai fini di una migliore comunicazione interpersonale. Infatti, tenuto conto che l'immagine ricostruita è gestibile esattamente come le altre originate da segnali che partono contemporaneamente da un dato oggetto supposto reale, è del tutto in linea con la sua attività organizzatrice delle esperienze e tutt'altro che un errore se il soggetto percipiente con atto istintivo decide di scegliere per uniformità la descrizione più semplice e considera contempora­neamente presenti le sorgenti dei segnali ricevuti là dove, invece, esse si manifestano in sequenza. Non diversamente dal fisico contemporaneo che formula non la teoria più vera (ciò che oggi appare un non senso) ma quella più semplice e funzionale.

Visto poi che anche gli strumenti adoperati dal fisico e da questo invocati come prova oggettiva spesso "vedono" delle realtà costruite al loro interno e non altrimenti individuabili, è, invece, il caso di chiedersi se gli oggetti, che riteniamo realmente esistenti fuori di noi e dai quali ci sembra di ricevere immagini, non siano anch'essi una proiezione esterna di ricostruzioni mentali dirette o mediate, la cui effettiva origine nessun “videotecnico” è ancora in grado di conoscere e rivelare.

Una proporzione chiamata divina

di Carmen Carano

(Istituto Tecnico Industriale G. Marconi”-Campobasso)

Gli antichi la chiamavano la “divina proporzione” perché ritenevano che fosse alla base di tutta la Creazione. È la proporzione continua in cui il medio proporzionale è una parte di un segmento (la sua ‘parte aurea”) e gli estremi sono l’intero segmento e la parte rimanente:

Tale proporzione è presente nelle forme più varie del Creato, da quella di conchiglie di molluschi a quella di galassie a spirale, dalla spaziatura tra le foglie lungo uno stelo e dei petali dei fiori all’accrescimento di una pigna, dalla molecola del DNA ai rapporti tra le dimensioni del corpo umano (tanto che oggi essa è usata persino nella chirurgia plastica e nei concorsi di bellezza).

La “divina proporzione” sembra alla base della percezione di equilibrio e armonia: da una indagine condotta su più persone alle quali sono stati mostrati rettangoli con diversi rapporti tra i lati, di fronte alla richiesta di indicare quale avesse in loro prodotto una maggiore sensazione di armonia, la preferenza, in modo netto, è andata al rettangolo con rapporto tra i lati pari a quello aureo.

Il rapporto tra un segmento e la sua parte aurea è sempre pari al numero irrazionale

(chiamato così in onore di Fidia, progettista del Partenone di Atene, che lo usò come canone estetico nella progettazione dell’opera:: da ciò, probabilmente deriva, il senso di profondo equilibrio che essa ispira) detto “numero aureo”, che ha affascinato studiosi di ogni epoca per le sue numerose e particolari proprietà.

Storicamente le prime applicazioni del rapporto aureo di cui si ha traccia risalgono a quasi 5000 anni fa, all’antico Egitto: si trovano rettangoli aurei nella stele del re Get e nelle piramidi. Ma i veri cultori del rapporto aureo furono i Greci:

Platone, nel Timeo, dice che i tre termini di una proporzione divina sono “tutti di necessità gli stessi e, poiché sono gli stessi, non sono che uno”.

Nel Rinascimento ci fu un’attenzione vivissima per il rapporto aureo che rappresentò per tutti gli artisti del periodo un canone di bellezza e di armonia per ogni composizione artistica (anche musicale) e architettonica (La pubblicazione più nota sul numero aureo, illustrata con disegni di Leonardo, è il “Divina Proporzione”, del matematico frate francescano Luca Pacioli (1445-1514)).

Sicuramente la percezione dell’armonia non si può ridurre solo alla presenza di un certo rapporto tra le dimensioni, ma viene da pensare che la naturale propensione per le forme in cui il rapporto tra le dimensioni sia quello aureo e il conseguente utilizzo dello stesso nelle sue opere, sia per l’uomo uno dei modi di tendere all’armonia del Creato e di tentare di riprodurla.

Società italiana di Scienze Matematiche e Fisiche

Fondata nel 1895

CONVEGNO

DI

STORIA DELLA MATEMATICA

Campobasso  13 – 14  marzo  2003

ÉVARISTE  GALOIS

 “Genio e incomprensione “

PROGRAMMA

GIOVEDI  13 marzo 2003 – ore 15.30 – Aula Magna del Convitto Nazionale “M. Pagano” - Campobasso

q       Saluto:  prof.  Andrea  Laforgia  (presidente della Mathesis Nazionale);

dott.ssa  M.Elena Toffolo (direttore editoriale Ed. Goliardiche)  

q       Presentazione del libro:

12 COMPITI SCOLASTICI DI ÉVARISTE GALOIS

di Sergio De Nuccio, Edizioni  Goliardiche

Relatori : prof.ssa  Margherita  Barile (Univ. di Bari)

prof. Mauro Palma (direttore di  ITERdell’ I.E.I.)

q       “ Conseguenze della Teoria di Galois nella matematica applicata moderna”

Relatore : prof. Franco  Eugeni  (Univ. di Teramo)

VENERDI 14 marzo 2003 – Aula Magna Ist. Tec. Comm.

                                       “ L. Pilla” – Campobasso

q       10.00 – 12.30  Incontro con gli alunni delle Scuole

                                Secondarie Superiori:

“La breve vita e i lavori scolastici di Évariste Galois”

Relatori : prof.ssa Giuseppina  Varone  (Univ. di Pescara)

 prof.  Sergio  De Nuccio  (presidente della sezione Mathesis di Campobasso)

q       15.30 – 18.30  Incontro con i docenti di matematica:

“ Le applicazioni della Teoria di Galois nella matematica moderna”

Relatori : Prof. Antonio Maturo  (Univ. di Pescara)

                       prof. Ioan  Tofan (Univ.“Al. I. Cuza”– Romania)