UN OGGETTO CHIAMATO SPAZIO

di Gabriele Rago – Campobasso

   Sino al finire dell'Ottocento la Fisica appariva come una solida costruzione unitaria fondata su quattro concetti fondamentali: lo spazio, il tempo, la materia ed il movimento. Questi per la maggior parte dei fisici erano oggetti primitivi, non ulteriormente analizzabili, facenti parte delle nozioni comuni e costituivano una specie di moderna teoria dei quattro elementi che caratterizzava il ben noto meccanicismo.

   Con ciò tuttavia non intendo dire che queste basi fossero altrettanto pacificamente acquisite in tutti gli altri ambienti in cui si era manifestato e si manifestava il pensiero, chè anzi esse furono elementi centrali del dibattito scientifico-filosofico presso gli antichi Greci e non hanno mai smesso di appassionare i pensatori successivi e in particolare  gli oppositori di Newton, tra i quali Leibniz, Huygens e Berkeley.

   Sta di fatto, però, che la reazione alla metafisica, tutta intesa a valorizzare l'evidenza sperimentale, ha raccolto i quattro elementi dal senso comune senza alcuna apprezzabile ripulitura e l'aspetto fondante e valido di questa scelta, più che da considerazioni critiche, è stato dimostrato "a posteriori" dai notevoli successi registrati dagli sviluppi della scienza galileiana e newtoniana.

   Solo più tardi, con l'estendersi delle sperimentazioni e delle scoperte a settori diversi, quali l'elettromagnetismo ed il comportamento delle particelle elementari, il modello meccanico è andato in crisi ed ha costretto i fisici a rivedere criticamente i concetti sui quali tale modello era fondato, nonchè a capire quanto ingenua fosse quella dottrina dei quattro elementi acriticamente accolti, a dispetto di tutto quanto in proposito aveva prodotto la storia del pensiero.

   Una prima fondamentale analisi critica  riguarda lo spazio e, per cogliere la sua natura, potremmo inizialmente credere di trovare un conforto nella geometria, la quale sembra occuparsene in via prioritaria. Però di fatto la geometria definisce lo spazio come un insieme di punti che godono di alcune proprietà assunte per via assiomatica e di altre che da queste si deducono per dimostrazione logica, senza con ciò nulla dire sulla natura dello spazio. Essa si presenta come una struttura linguistica che non ha senso fisico fin quando non viene interpretata. Ed il motivo del contendere è proprio questa interpretazione. I punti sono interpretabili come eventi e percezioni o come elementi di una realtà indipendente nella quale eventi e percezioni si collocano?

   Nei suoi scritti Einstein ha osservato che lo spazio è una libera costruzione della mente umana tendente a realizzare un ordinamento degli eventi e delle percezioni, tale da consentirci una migliore individuazione, comprensione e gestione degli stessi. Essa può articolarsi in due diversi concetti, che, in sostanza, appaiono distinti solo per le contrastanti interpretazioni che storicamente sono state loro assegnate.

   Il primo di questi riflette le relazioni che si possono stabilire tra gli elementi sperimentati e che, a seconda delle proprietà che esse presentano, vengono denominate intervalli,  distanze  o spostamenti.  Queste relazioni, poi, possono essere integrate in una struttura relazionale (space), mediante la quale indirettamente è possibile stabilire la posizione di ciascun oggetto rispetto al complesso degli altri (place). Si giunge così ad un certo concetto di spazio che segue logicamente l'esperienza e le cui relazioni sono studiate da una opportuna geometria validata dalla risultanze sperimentali. Questo è, in fondo, il moderno concetto di spazio come sistema di relazioni interconnesse, che cominciò ad affiorare nella definizione di posizione data da Aristotele, venne poi sostenuto da Teofrasto e, malgrado il diverso corso della scienza, giunse a chiarirsi nella sua essenza con il  principium individuationis   di Locke e l' ordo coexistendi   di Leibniz.

   Il secondo concetto, invece, indipendentemente dal tipo di geometria che lo descrive, sia essa euclidea o non, rappresenta lo spazio come un contenitore universale, omogeneo ed isotropo, illimitato in ogni direzione, immutabile e rigido, indipendente dal tempo, che contiene in sè tutti gli oggetti fisici ed è totalmente passivo ed indifferente rispetto a questi suoi contenuti. E' subito visto che questo secondo tipo di spazio, a meno di risolversi  nel precedente in quanto puro e semplice schema di previsione di una localizzazione, acquista una sua realtà oggettiva che si inquadra logicamente nell'esperienza e per ciò stesso pone notevoli e irrisolti problemi.

   Oggi sappiamo che lo spazio contenitore e reale può concepirsi solo ricommettendo il principale errore dei pensatori greci, che consiste nella ipostatizzazione dei prodotti mentali e cioè nel vedere questi come una realtà esterna indipendente dalla mente che li ha generati. Errore che si è riprodotto nel tempo, perchè è del tutto naturale e viene continuatamente commesso da ognuno di noi nella primissima infanzia, quando, per esigenze di sopravvivenza, siamo costretti a farci un'idea, anche errata ma funzionale, di come è fatto il mondo. Errore nel quale sono ingenuamente caduti anche Galileo e Newton.

   Però lo spazio concepito come realmente esistente va a collocarsi tra gli oggetti dell'esperienza e quindi va necessariamente a scontrarsi con la materia, alla quale nel corso della storia del pensiero scientifico esso è sempre apparso correlativo. Entrambi i concetti, infatti, nascono dalla più generale contrapposizione di essere  e di non essere  ed inizialmente lo spazio si configura come ciò che non è materia eppure esiste. Questo strano concetto, che oggi chiamiamo vuoto,  che assegna un'esistenza al nulla e che solo la potenza intellettiva dei Greci poteva produrre, fu necessario agli Atomisti per consentire la dinamica dei loro atomi, ma fu subito bloccato dall'autorevole pensiero di Aristotele, fino a quando non riapparve in seno alla fisica del Rinascimento nella forma più moderna tramandata da Lucrezio e cioè come spazio non più alternativo alla materia ma inclusivo di questa. Ed è proprio dalla correlazione spazio-materia che nascono le incongruenze che portano all'inammissibilità dello spazio newtoniano.

   Una di queste è appunto quella rilevata da Clifford con il paradosso che porta il suo nome. E' noto che la riduzione in scala di un oggetto o di un sistema fisico ne altera notevolmente i comportamenti. Una spiga di grano, ad esempio, anche se agitata dal vento, si erge e si autosostiene senza problemi, mentre un altro vegetale di identica struttura, che in proporzione fosse cento volte più grande, si affloscerebbe istantaneamente anche senza la complicità del vento. Analogamente le avventure di Gulliver sono un esempio di pessima fantascienza, perchè i lillipuziani dovrebbero saltare come grilli ed i giganti invece dovrebbero crollare sotto il loro stesso peso. Ciò vuol dire che la materia ha dimensioni assolute riconoscibili dal tipo di fenomeni che si osservano. Viceversa lo spazio ha dimensioni relative, perchè, se si riducessero di un certo fattore le dimensioni di tutti gli oggetti, compresi anche l'osservatore ed i suoi strumenti di misura, da un punto di vista puramente spaziale, non se ne accorgerebbe nessuno.

   Altro difetto di correlatività sta nel fatto che allo spazio vengono attribuiti caratteri di continuità e, quindi, in particolare di divisibilità infinita che la materia e l'energia hanno mostrato di non possedere.

   Ma la crisi più grave, che storicamente ha decretato la fine dello spazio contenitore, è la comparsa del concetto di campo ed in particolare la scoperta dei campi elettromagnetici. La vanificazione dell'esistenza dell'etere, la riduzione dei campi a modifiche dello spazio e la formulazione relativistica delle equazioni del campo hanno dimostrato essere illegittime sia la distinzione tra spazio e materia e sia la concezione di un ente indifferente ai suoi contenuti. Resta invece legittima la struttura relazionale mentalmente prodotta con la quale "a posteriori" lo spazio-materia viene descritto nei suoi comportamenti.

   L'analisi potrebbe spingersi a mostrare come anche il tempo ed il moto vadano a confluire nell'unica realtà materiale e come alcuni dei caratteri a questa attribuiti, come ad esempio la rigidità, siano in realtà caratteri propri delle struttura che la modellizza, ma ciò ci porterebbe molto lontano. Qui, invece, interessa sottolineare che queste considerazioni, in apparenza puramente accademiche, hanno al contrario una notevole importanza didattica.

   Troppo frequentemente, infatti, l'insegnante cerca di semplificare e rendere più accessibile il proprio intervento didattico appoggiandosi a quei concetti che fanno parte del senso comune e che spesso, come accade appunto per un certo concetto di spazio, in età prescolare nascono sbagliati e non idonei a comprendere la diversa visione del mondo che la scienza moderna ci propone. Pertanto discutendo questi errori ci auguriamo che egli, pur consapevole delle possibili maggiori difficoltà, ometta il loro tacito avallo e si assegni, invece, il compito di correggerli.

CALCOLO DEL VOLUME DEL SOLIDO GENERATO DALLA ROTAZIONE DI UN TRAPEZIO INTORNO A UNO DEI SUOI LATI CON IL TEOREMA DI GULDINO

di  Domenico Di Biase -  Bojano   (CB)

Teorema di Guldino: Il volume del solido generato dalla rotazione di una figura piana intorno ad una retta che non l’attraversi, è dato dal prodotto dell’area della superficie della figura per la lunghezza della circonferenza descritta dal baricentro della figura nella rotazione.

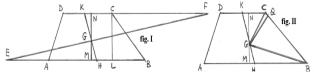
Per applicare il teorema di Guldino dobbiamo procurarci -in funzione dei lati, delle basi e dell’altezza- le distanze del baricentro del trapezio dalle basi e dal lato obliquo. Ricordiamo, senza darne la dimostrazione, la costruzione del baricentro del trapezio.

Si prolunghi (cfr.fig.I) la base minore DC, dalla parte di C, di un segmento CF uguale alla base maggiore AB; e, viceversa si prolunghi la base maggiore AB, dalla parte di A di un segmento EA uguale alla base minore DC; detti K e H i punti medi, rispettivamente, della base minore e della base maggiore, il baricentro G, del trapezio, coincide con l’intersezione del segmento EF con il segmento HK.

Siano  rispettivamente le misure della base maggiore, della base minore, del lato obliquo  CB, dell’altezza CL del trapezio. Applicando il teorema delle altezze ai triangoli simili EGH e KGF si ha (fig. I):

e passando alle misure:     

   (1)

Applicando il componendo e tenendo presente che , si ottiene:

  e      (2)

che esprimono le distanze del baricentro G, rispettivamente, dalla base maggiore e da quella minore.

Con le notazioni della figura (II) si ha:

 ; ; .

Per quanto riguarda la distanza del baricentro del trapezio dal lato obliquo CB si ottiene:

     (3)

Se con  indichiamo il volume del solido ottenuto dalla rotazione del trapezio intorno, rispettivamente, alla base maggiore, alla base minore ed al lato obliquo CB, applicando il teorema di Guldino e tenendo presente che , si ha:

; ; .

espressioni che possono essere facilmente memorizzate.