Un Asteroide in 2°I

 copia della pagina per stampa

Realizzato da Julia, Katia, Letizia, Alessandro,Martina.

Abbiamo letto che uno dei primi casi di applicazione del Teorema di Pitagora si trova in una tavoletta babilonese del 1800 a.C.

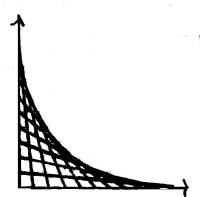
Il problema è questo: <<Un bastone lungo 30 unità è appoggiato a un muro. Poi scivola di 6 unità. Di quanto il piede del bastone si è allontanato dalla base del muro?>>. Applicando il Teorema di Pitagora varie volte si ottiene che il piede del bastone dista dalla base del muro lunghezze diverse come risulta dal grafico che ci fa vedere la posizione del segmento sempre diversa. 

Indichiamo con p la posizione del bastone

p1=√30^2-29^2=7,681945784

p2=√30^2-27^2=13,07669683

p3=√30^2-24^2=18

p4=√30^2-21^2=21,42428529

p5=√30^2-18^2=24

p6=√30^2-15^2=25,98076211

p7=√30^2-12^2=27,49545417

p8=√30^2-9^2=28,61817604

p9=√30^2-6^2=29,39387691

p10=√30^2-3^2=29,84962311

p11=√30^2-1^2=29,9833287

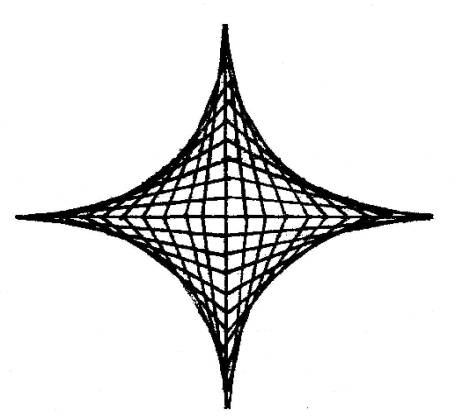
Ci accorgiamo che questi segmenti inviluppano una curva: è un quarto di asteroide. Quindi riproducendo per simmetria ciò che abbiamo ottenuto nel primo quadrante, appare la figura sotto riportata: un intero asteroide.

Per i virtuosi del calcolo (non è il nostro caso perché siamo solo dei miracolati) riportiamo queste esplosioni numeriche!!!!!!

√30^2-28^2= 10,77032961

√30^2-26^2= 14,96662955

√30^2-25^2= 16,58312395

√30^2-23^2= 19,26136028

√30^2-22^2= 20,39607805

√30^2-20^2= 22,36067977

√30^2-19^2= 23,21637353

√30^2-17^2= 24,71841419

√30^2-16^2= 25,37715508

√30^2-14^2= 26,53299832

√30^2-13^2= 27,03701167

√30^2-11^2= 27,91057147

√30^2-10^2=28,28427125

√30^2-8^2=28,91366459

√30^2-7^2=29,17190429

√30^2-5^2=29,58039892

√30^2-4^2=29,73213749      

√30^2-2^2=29,93325909